
Once you learn how to use regression, you will be able to estimate the parameters - the slope and intercept - of the function that links two or more variables. Regression analysis is one of the most used and most powerful multivariate statistical techniques for it infers the existence and form of a functional relationship in a population. If there is a relationship between studying and grades, the location of that distribution of grades will change in an orderly manner as you move from lower to higher levels of studying. For each level of amount studied, there will be a distribution of grades. Some students are taking harder courses, like chemistry or statistics some are smarter some study effectively and some get lucky and find that the professor has asked them exactly what they understood best. Notice that even if students who study more make better grades, the relationship in the population would not be perfect the same amount of studying will not result in the same grades for every student (or for one student every time).

You could then complete your inference and test your hypothesis by gathering a sample of (amount studied, grades) data from some students and use regression to see if the relationship in the sample is strong enough to safely infer that there is a relationship in the population.

If you say that students who study more make better grades, you are really hypothesizing that there is a positive relationship between one variable, studying, and another variable, grades. These relationships are seldom exact because there is variation caused by many variables, not just the variables being studied. For example, if you wanted to generate a line of best fit for the association between height and shoe size, allowing you to predict shoe size on the basis of a person's height, then height would be your independent variable and shoe size your dependent variable).Regression analysis, like most multivariate statistics, allows you to infer that there is a relationship between two or more variables. To begin, you need to add paired data into the two text boxes immediately below (either one value per line or as a comma delimited list), with your independent variable in the X Values box and your dependent variable in the Y Values box. This calculator will determine the values of b and a for a set of data comprising two variables, and estimate the value of Y for any specified value of X.
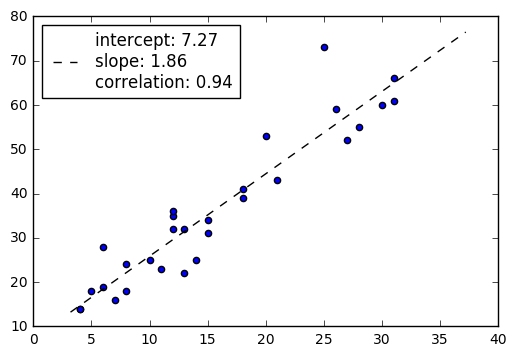
The line of best fit is described by the equation ŷ = bX + a, where b is the slope of the line and a is the intercept (i.e., the value of Y when X = 0). This simple linear regression calculator uses the least squares method to find the line of best fit for a set of paired data, allowing you to estimate the value of a dependent variable ( Y) from a given independent variable ( X).


 0 kommentar(er)
0 kommentar(er)
